Schedule
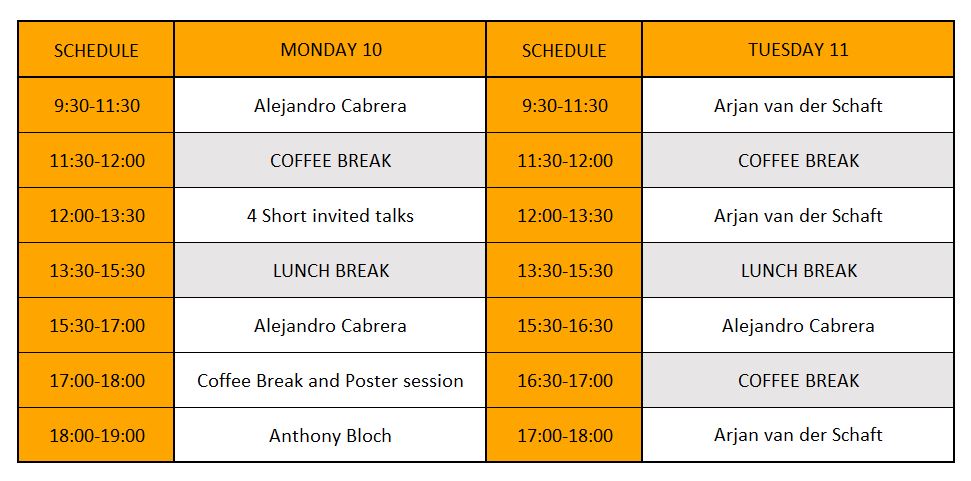
Short talks on Monday, July 10
- 12:00 Miguel Ángel Berbel (Universidad Pontificia Comillas, Spain).
Title: The link between Lagrange–Poincaré and Poisson–Poincaré reduction. Abstract - 12:20 Eugenio Petit Valdes (Univerity of Trento, Italy).
Tittle: To be announced. - 12:40 Bartosz Maciej Zawora (University of Warsaw, Poland).
Title: On k-polycosymplectic Marsden-Weinstein reductions. Abstract - 13:10 Jordi Gaset (Universidad Politécnica de Madrid).
Title: Multicontact Systems.
Abstract: Multicontact systems are a generalization of contact mechanics for field theories. We will show the principal properties of these systems and some applications.
Poster abstracts, July 10
- Title: Contracting forced mechanical systems
Authors: Alexandre Anahory Simoes and Leonardo Colombo
Abstract: We address the problem of identifying contracting systems among dynamical systems appearing in mechanics. First, we introduce a sufficient condition to identify contracting systems in a general Riemannian manifold. Then, we apply this technique to establish that a particular type of dissipative forced mechanical system is contracting, while stating immediate consequences of this fact for its stability. Finally, we use the previous results to study the stability of particular types of Contact and Nonholonomic systems. - Title: An energy-momentum method for ordinary differential equations with an underlying k-polysymplectic structure
Authors: L. Colombo, J. de Lucas, X. Rivas, B.M. Zawora
Abstract - Title: Virtual Nonholonomic Constraints: A Geometric Approach
Authors: Efstratios Stratoglou
Abstract: Virtual constraints are relations imposed on a control system that become invariant via feedback control, as opposed to physical constraints acting on the system. Nonholonomic systems are mechanical systems with non-integrable constraints on the velocities. In this work, we introduce the notions of virtual linear, affine and nonlinear nonholonomic constraints in a geometric framework which are, in the first two cases controlled invariant distributions and in the nonlinear case a controlled invariant submanifold and we show the existence and uniqueness of a control law preserving each of these structures in any case. We illustrate the theory with various examples and present simulation results for an application. - Title: Learning cost functions based on data as a quadratic programming problem
Authors: Omayra Yago Nieto, Alexandre Anahory and Leonardo Colombo
Abstract: We propose two methods based on quadratic programming to approximate either the unknown Hamiltonian or Lagrangian cost function of a mechanical system with a given optimal controller. We incorporate the error in the approximation to build a data-driven differential inclusion, that is suitable for control purposes. We illustrate the results by different polynomial basis and by the inverted pendulum case. - Title: On the invariants of Numerical Semigroups
Authors: Isabel Fernández



