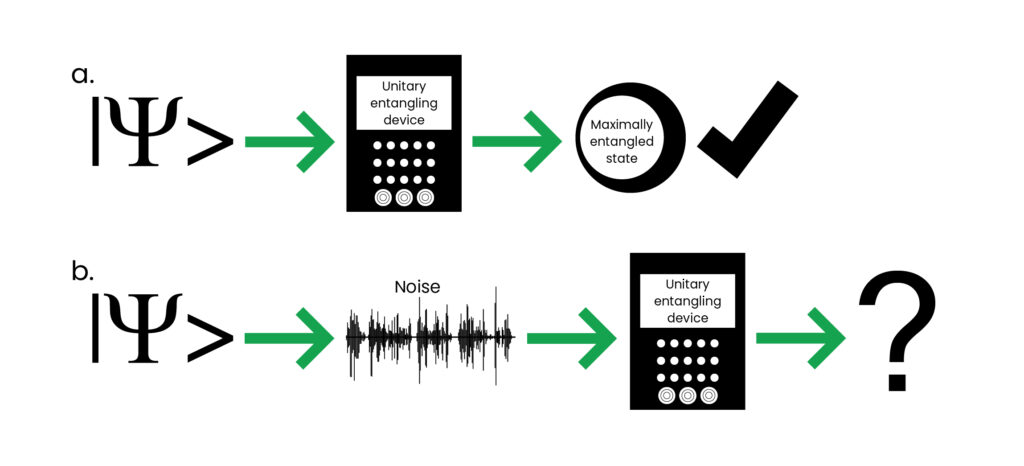
Representación gráfica del resultado de De Vicente. Crédito: Laura Moreno-Iraola (ICMAT)
Para muchas aplicaciones tecnológicas cuánticas interesa obtener partículas entrelazadas –es decir, partículas cuánticas entre las que existe una correlación muy fuerte, un fenómeno sin análogo en el mundo clásico–. El estado más útil para todas estas aplicaciones, independientemente de la tarea particular a realizar, es el llamado estado máximamente entrelazado, cuya existencia, en ausencia de ruido, se conoce desde hace tiempo. También se sabe que, en situaciones realistas, en las que la presencia de ruido es inevitable, este estado es inalcanzable. Ahora, se ha demostrado algo más: “No puede existir ninguna noción universal de entrelazamiento máximo fuera del escenario idealizado sin ruido, incluso cuando el ruido es arbitrariamente pequeño. En este caso, el mejor estado entrelazado que se puede obtener dependerá de la aplicación concreta para la que se vaya a utilizar”. Así se recoge en un reciente resultado de Julio de Vicente, profesor titular de la Universidad Carlos III de Madrid y miembro del ICMAT, que publica esta semana Physical Review Letters. De Vicente nos habla sobre ello en la siguiente entrevista.
Ágata Timón García-Longoria (ICMAT)
Pregunta: ¿Qué es el estado máximamente entrelazado y por qué es importante?
Respuesta: El entrelazamiento es una forma de correlación muy fuerte que se puede dar entre dos partículas cuyo comportamiento venga descrito por las leyes de la mecánica cuántica. Este fenómeno no tiene análogo en la mecánica clásica y está detrás de muchas de las prometedoras aplicaciones de las tecnologías cuánticas. Uno de los ejemplos más llamativos es el del establecimiento de una clave secreta para aplicaciones criptográficas. En muchos escenarios, la verificación de que las dos partes implicadas comparten estados entrelazados es la piedra angular de la seguridad del protocolo y garantiza que la comunicación no puede ser descifrada por un tercero. Otro ejemplo es el teletransporte cuántico, que permite transmitir un estado cuántico desconocido a una localización remota mediante un canal de comunicación clásico. Sin entrelazamiento estas aplicaciones fracasan: no tenemos ninguna garantía de que la comunicación no esté siendo espiada ni de fidelidad en el teletransporte.
Como muchas otras propiedades físicas, el entrelazamiento se manifiesta en diferentes formas y, dentro de todos los posibles estados que describen un sistema cuántico de dos partículas –llamado bipartito–, existen distintos grados de entrelazamiento. Entre todos ellos, hay uno que es el estado máximamente entrelazado: el mejor estado entrelazado disponible, independientemente de la aplicación particular que se tenga en mente. En los ejemplos anteriores, de criptografía y teletransporte cuánticos, el estado máximamente entrelazado garantiza el mayor nivel de privacidad posible y hace que el teletransporte sea perfecto, respectivamente. En términos matemáticos, este estado maximiza todas las posibles medidas que cuantifican, de alguna manera, el entrelazamiento.
P: ¿Es posible obtener este estado? ¿Qué dice tu trabajo al respecto?
R: En la práctica, debido a la presencia de ruido, este estado es inalcanzable. Sin embargo, podríamos preguntarnos: dada una fuente de ruido bien caracterizada, una vez fijado el nivel de ruido, ¿existe un estado entrelazado que sea el mejor? Mi trabajo responde a esta pregunta de manera negativa. No puede existir ninguna noción universal de entrelazamiento máximo fuera del escenario idealizado, incluso cuando el ruido es arbitrariamente pequeño. En este caso, el mejor estado entrelazado que se puede obtener dependerá de la aplicación concreta para la que se vaya a utilizar.

Julio de Vicente es profesor titular de la Universidad Carlos III de Madrid y miembro del ICMAT
P: Hasta el momento, ¿qué se sabía de esta cuestión?
R: En 2001 se había demostrado que, para cualquier nivel de ruido dado, existe un estado que maximiza diversas medidas de entrelazamiento de relevancia. Esto había llevado a albergar la esperanza de que existiera un estado máximamente entrelazado en el caso ruidoso, pero para ello era necesario demostrar que este estado maximiza cualquier medida de entrelazamiento, y no solo unas cuantas. Sin embargo, estas cantidades son excepcionalmente complicadas de evaluar y, de hecho, sabemos que llevan a problemas computacionalmente difíciles. Por ello, no se había avanzado mucho en esta pregunta.
P: ¿Cómo has abordado tú la cuestión?
R: En este trabajo, la idea primordial es, en vez de pegarse con estos problemas tan duros, considerar una relación de orden entre estados, que fija que una medida de entrelazamiento sea mayor o menor. Lo que hemos demostrado es que es imposible que haya un elemento máximo, mejor que cualquier otro. Una vez hecho esto, obtuvimos automáticamente medidas de entrelazamiento particulares, que sirven como contraejemplo a la esperanza surgida en 2001.
P: Y esto, ¿qué implica en relación con la criptografía y el teletransporte cuántico?
R: Si usamos estados «menos» entrelazados, todavía es posible la criptografía y el teletransporte, pero el proceso para destilar la clave secreta es más ineficiente en el primer caso y la transmisión no es completamente fiel en el segundo. Y, a diferencia del caso sin ruido, el resultado de este trabajo indica que, para un mismo nivel de ruido, el estado óptimo para hacer criptografía puede ser diferente del estado que mejor teletransporta.
P: En la práctica, ¿se han observado estos fenómenos?
R: Yo no soy un experto en esta parte del campo, pero la preparación experimental de estados entrelazados para sistemas de dos partículas está muy avanzada. Los primeros experimentos se hicieron en los años 70 del siglo pasado, para verificar violaciones de las llamadas desigualdades de Bell. De hecho, en 2022 se concedió el premio Nobel a Alain Aspect, John F. Clauser y Anton Zeilinger por su trabajo pionero en la implementación experimental de estados entrelazados con fotones, para aplicaciones de teoría de la información cuántica. En la actualidad es posible preparar el estado máximamente entrelazado de dos partículas en sistemas físicos muy diferentes: como la polarización de fotones, los niveles de energía de iones atrapados o en circuitos superconductores. Los experimentos realizados en estos casos alcanzan fidelidades muy altas, incluso por encima del 99%, aunque nunca se llega al 100%, es decir, al estado máximamente entrelazado. Esto ha permitido resultados espectaculares como, por ejemplo, teletransportar desde la isla de La Palma a Tenerife –entre las que hay más de 140 kilómetros– o incluso desde la Tierra a un satélite en el espacio –a más de 1000 kilómetros–.
P: ¿Cuáles son los próximos pasos en este tema?
R: En el contexto concreto de mi trabajo, cabe decir que la demostración de la inexistencia de un estado máximamente entrelazado en el caso ruidoso se basa en medidas de entrelazamiento construidas ad hoc, sin un significado operacional claro. Sería interesante identificar protocolos específicos de información cuántica donde el estado óptimo a un mismo nivel de ruido cambia. Por otro lado, el resultado se refiere a una forma concreta, muy razonable, pero específica, de entender lo que significa «el mismo nivel de ruido». Se podría investigar si el resultado sigue siendo cierto para otras nociones. Desde una perspectiva más general, un reto importante es avanzar más en nuestra comprensión de la estructura del entrelazamiento en el caso multipartito, que es mucho más compleja, y, en particular, entender mejor para qué tareas supone una ventaja y poder desarrollar nuevos protocolos y aplicaciones.
Referencia:
“Maximally entangled mixed states for a fixed spectrum do not always exist”, Julio de Vicente. Physical Review Letters. DOI: 10.1103/PhysRevLett.133.050202
Julio de Vicente
Julio de Vicente es profesor titular de la Universidad Carlos III de Madrid y miembro del ICMAT. Sus intereses de investigación se centran en la teoría de la información cuántica, especialmente en la teoría del entrelazamiento, la no-localidad y las teorías de recursos cuánticos.
Licenciado en Ciencias Físicas por la Universidad Autónoma de Madrid en 2002, obtuvo su doctorado en Matemáticas por la Universidad Carlos III de Madrid en 2008. Ha ocupado posiciones postdoctorales en la Universitat Autònoma de Barcelona (2008-2010) y en la Universität Innsbruck (2010-2013). Desde 2013 trabaja en el Departamento de Matemáticas de la UC3M, inicialmente como profesor ayudante doctor y, desde 2019, como profesor titular.
