Los horizontes de las matemáticas, con Motohico Mulase (Universidad de California Davis (EE. UU.))

Motohico Mulase es experto en sistemas integrables, geometría algebraica compleja, análisis complejo, física matemática y geometría diferencial.
Motohico Mulase (Universidad de California Davis (EE. UU.)) es el ponente del Coloquio Conjunto ICMAT-UAM-UCM-UC3M que se celebra el 11 de octubre. Su charla, “Miraculous Integer Sequences”, explora dos fascinantes secuencias de números enteros: la de los números de Catalán y la de invariantes de Gromov-Witten de género 0 de una cierta variedad algebraica. En ellas, aparecen conexiones con la cosmología, con la física cuántica y con la misteriosa función zeta de Riemann. El evento es a la 13:00 en el Aula Magna Miguel de Guzmán de la Facultad de Ciencias Matemáticas de la Universidad Complutense de Madrid y también puede seguirse online en el siguiente enlace.
Ágata Timón García-Longoria (ICMAT)
En la escuela nos enseñan secuencias –es decir, colecciones ordenadas– de números enteros: la de los números pares, o los impares, la de los primos –que tantos misterios entraña–, la de los cuadrados perfectos… Algunas son especialmente interesantes, como, por ejemplo, la famosa secuencia de Fibonacci: (1, 1, 2, 3, 5, 8, …). En sus términos –cada uno de ellos se construye sumando los dos anteriores–, emerge el número áureo –a medida que avanza la secuencia de Fibonacci, la división de dos términos consecutivos se acerca cada vez más a este valor irracional–. Además, esta colección de números también aparece en fenómenos naturales, por ejemplo, al observar los patrones de crecimiento de las hojas, pétalos de flores y ramas de las plantas, o la distribución de semillas en girasoles. El matemático Motohico Mulase, investigador de la Universidad de California Davis (EE. UU.), se dedica a descubrir las propiedades más asombrosas de este tipo de secuencias.
Una de las secuencias estudiadas por Mulase es la de los números de Catalan. “Aparece en muchos problemas combinatorios y también en la clasificación de agujeros negros en astrofísica”, explica Mulase. “La función generadora de los números de Catalan [en la imagen inferior] satisface una ecuación diferencial y, si aplica una simple transformación sobre ella –la transformada de Laplace, que corresponde a lo que se denomina la simetría especular–, se obtiene otra ecuación diferencial –su pareja simétrica en el espejo–. Pues bien, esta ecuación simétrica resulta ser una ecuación de Schrödinger”, descubre Mulase. Se trata de una de las ecuaciones fundamentales de la mecánica cuántica, que describe cómo evoluciona a lo largo del tiempo el estado cuántico de un sistema físico. “Lo más fascinante es que esta ecuación conoce la topología de los llamados espacios de moduli de todas las superficies de Riemann”, añade.
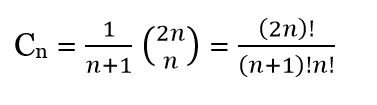
Los números de Catalan pueden obtenerse mediante la siguiente fórmula, dando a n valores naturales.
Otra de las secuencias de enteros sobre las que ha investigado es la de los invariantes de Gromov-Witten de género 0 de una cierta variedad algebraica. “Estas cantidades tienen su origen en la teoría cuántica de campos”, afirma Mulase. “Cuando miramos al cielo nocturno, nos preguntamos por la inmensidad del universo y su asombrosa belleza. El deseo de comprender mejor nuestro universo llevó a los físicos a descubrir un nuevo conjunto de indicadores de la estructura del universo: los invariantes de Gromov-Witten”, relata. “En ese momento, se incorporaron a las matemáticas, como un nuevo tipo de invariante de la geometría simpléctica”, afirma.
“Sorprendentemente, esa misma secuencia de números enteros fue descubierta, hace casi medio siglo, por el teórico de números Roger Apéry, en su demostración de la irracionalidad del valor de la famosa función zeta de Riemann en 3”, declara Mulase. “La función zeta de Riemann es una de las funciones más misteriosas, y no se sabe casi nada de sus valores en números enteros impares positivos. Sólo por su valor 3, sabemos que es irracional, gracias a la demostración de Apéry”, señala el matemático.
Para demostrar este profundo resultado, fue clave la misma sucesión de enteros que idearon los físicos teóricos. “La usó para construir una sucesión racional rápidamente convergente que se aproxima al valor de la función zeta en 3. Como la convergencia de esta aproximación es tremendamente rápida, con un simple teorema de teoría de números pudo afirmar que la función zeta en 3 tiene que ser irracional”, explica.
“Este valor de la función zeta en tres aparece en muchos lugares de la física, como el momento magnético anómalo del electrón, y de la geometría, pero aquí se muestra una historia diferente: ¡El invariante simpléctico de un espacio geométrico parece conocer la irracionalidad de zeta(3)!”, exclama Mulase.
“Así, mirando al cielo estrellado en la noche, aparecen estas fronteras de las matemáticas modernas, en las que interactúan la geometría, la teoría de números, las ecuaciones diferenciales y la topología. Los cielos nos invitan a apreciar la belleza oculta en las diferentes partes de las matemáticas y sus entrelazamientos”, concluye el investigador.
Motohico Mulase
Motohico Mulase nació en Kanazawa, Japón. Se licenció en la Universidad de Tokio y realizó su doctorado en la Universidad de Kioto. Tras un breve periodo en la Universidad de Nagoya, se trasladó a Estados Unidos en 1982 como becario en la Universidad de Harvard. Ocupó puestos en el Instituto de Investigación de Ciencias Matemáticas de Berkeley, la Universidad de Stony Brook, la Universidad de California en Los Ángeles y el Instituto de Estudios Avanzados de Princeton. En 1989 obtuvo una plaza de profesor titular en la Universidad de California, Davis,donde es catedrático desde 1991. En esta institución, Mulase ha sido director del Departamento de Matemáticas, decano de la Facultad de Ciencias Matemáticas y Físicas y, desde 2019, es Profesor Distinguido de Matemáticas. Ha ocupado puestos de investigador visitante en numerosas instituciones, entre ellas el Max-Planck-Intitut für Mathematik en Bonn (Alemania) y l’Institut des Hautes Études Scientifiques en París (Francia).
Coloquio conjunto de matemáticas “Miraculous Integer Sequences”, Motohico Mulase (University of California, Davis). Viernes 11 de octubre de 2024, a la 13:00 en el Aula Magna Miguel de Guzmán de la Facultad de Matemáticas de la Universidad Complutense de Madrid y en el siguiente link.
Abstract:
In this Colloquium, I will survey two such sequences, and explain their unexpected miracles.
The first one is the Catalan numbers. I will explain how this integer sequence leads us to two differential equations, their mirror-symmetric relations, and the quantization behind the scenes. We present Lauren polynomials that give solutions to these equations.
The miracle here is that these Laurent polynomials know the topological invariants of the moduli space of pointed Riemann surfaces, calculated by Harer-Zagier, Witten, and Kontsevich.
The second example is analogous to the first one in the sense that it is an integer sequence of genus 0 Gromov-Witten invariants of a particular algebraic 3-fold. We have again two differential equations. The contrast is that although we know mirror symmetric and quantization relation between these equations, the key mechanism to calculate general GW invariants is still missing. The miracle here is that this particular integer sequence knows why Riemann zeta at 3 is irrational, the work of Apery.
